数据结构学习笔记

发表于 更新于 分类于 本文字数： 1.7k 阅读时长 ≈ 6 分钟
数据结构学习记录

绪论

算法的定义

解决特定问题求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令表示一个或多个操作。

算法的特性

  • 有限性: 一个算法必须保证执行有限步之后结束.
  • 确切性: 一个算法的每一步骤必须有确切的定义.
  • 输入: 一个算法有零个或多个输入, 以刻画运算对象的初始情况, 所谓零个输入是指算法本身给定了初始条件.
  • 输出: 一个算法有一个或多个输出. 没有输出的算法毫无意义.
  • 可行性: 一个算法的任何计算步骤都是可以被分解为基本可执行的操作，每个操作都能够在有限时间内完成.

算法的设计要求

算法设计一般要求满足以下几点：

1. 正确性：算法的执行结果应当满足预先规定的功能和性能要求。即算法应当满足具体问题的需求，设计或选择的算法应当能够正确地反映这种需求，这是衡量算法正确与否的准则。

2. 可读性：一个算法应当思路清晰、层次分明、易读易懂。算法主要是为了人的阅读与交流，其次才是机器执行。可读性好有助于人对算法的理解，而晦涩难懂的算法易于隐藏较多的错误，最终难以调试和修改。

3. 健壮性：当输入不合法的数据时，应当作适当处理，不致于引起严重后果。例如当输入数据不在允许的范围时，算法应能适当地作出反应或处理，而不会产生莫名其妙的输出结果。

4. 高效性：有效地使用存储空间和有高效的时间效率。效率是指的执行时间，如果对于一个问题有多个算法可以解决，那么执行时间短的算法效率就高。存储量需求是指算法执行过程中所需的最大存储空间。一个理想的算法应该是数据所占用的存储空间较小而数据处理的速度较快。

时间复杂度计算规则

  • 加法规则

    \[T(n)=T_1(n)+T_2(n)=O(f(n))+O(g(n))=O(max(f(n),g(n)))\]

  • 乘法规则

    \[T(n)=T_1(n)\times T_2(n)=O(f(n))\times O(g(n))=O(f(n)\times g(n))\]

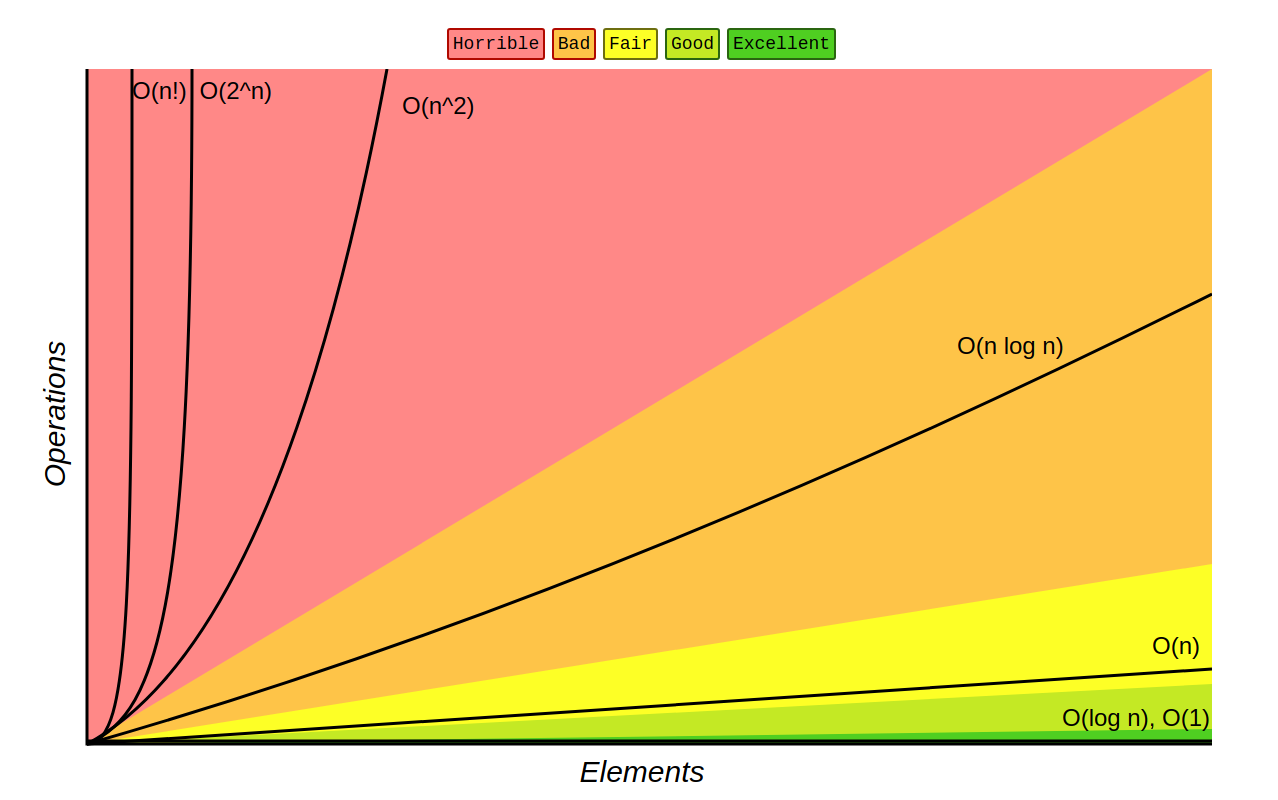
常见的时间复杂度大小顺序

\[O(1)<O(\log n)<O(n)<O(n\log n)<O(n^2)<O(n^3)<\cdots <O(n^k)<O(2^n)<O(n!)<O(n^n)\]

Quick Review: Big-O Notation

线性表

顺序表的插入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include <cstdio>
#include <cstdlib>

#define ElemType int

struct SqList
{
	ElemType* ptr;  //数组指针
	int length;     //元素个数
	int capacity;   //数组容量
};

int InitSqList(SqList*& L, int capacity)
{
	if (capacity <= 0)
		return -1;
	L = (SqList*)malloc(sizeof(SqList));
	if (!L)
		return -1;
	L->ptr = (ElemType*)malloc(capacity * sizeof(ElemType));
	if (!L->ptr)
		return -1;
	L->length = 0;
	L->capacity = capacity;
	return 0;
}

int InsertSqList(SqList* L, int index, ElemType data)
{
	if (index < 0 || index > L->length || L->length == L->capacity)
		return -1;	//插入失败: 索引错误或容量已满
	else if (index == L->length)	//插入到线性表最后一个元素的后一个
		L->ptr[index] = data;
	else
	{
		for (int i = L->length - 1; i >= index; i--)
			//元素从后往前依次向后移动1次, 从后往前避免覆盖
		{
			L->ptr[i + 1] = L->ptr[i];
		}
		L->ptr[index] = data;
	}
	L->length++;
	return 0;
}

void DisplaySqList(SqList* L)
{
	if (L->length == 0)
	{
		printf("[Blank SqList]\n");
		return;
	}
	for (int i = 0; i < L->length; i++)
		printf("%d ", L->ptr[i]);
	putchar('\n');
}


int main()
{
	SqList* s = nullptr;
	InitSqList(s, 100);
	DisplaySqList(s);
	InsertSqList(s, 0, 1);
	InsertSqList(s, 1, 2);
	InsertSqList(s, 2, 4);
	InsertSqList(s, 2, 3);
	InsertSqList(s, 0, 0);
	DisplaySqList(s);
}

/*
[Blank SqList]
0 1 2 3 4

*/

循环单链表插入(尾指针表示, 带头节点)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include <cstdio>
#include <cstdlib>


#define ElemType int

struct Node
{
    ElemType data;
    Node* next;
};



int InitLinkedList(Node*& L)
{
    L = (Node*)malloc(sizeof(Node));
    if (!L)
        return -1;
    L->next = L;
    return 0;
}

int InsertLinkedList(Node*& L, int index, ElemType data)
{
    if (index < 0)
        return -1;
    Node* head = L->next;

    int i = -1;
    Node* p = head;
    do
    {
        if (i == index - 1)     //如果当前节点为要插入位置的前一个节点
        {
            Node* newNode = (Node*)malloc(sizeof(Node));
            if (!newNode)
                return -1;
            newNode->data = data;
            newNode->next = p->next;
            p->next = newNode;
            if (newNode->next == head)  //如果新插入的节点是尾节点, 那么把尾指针指向新节点
                L = newNode;
            return 0;
        }
        p = p->next, i++;
    } while (p != head);

    return -1;  // 如果整个循环链表中都没有目标位置, 就返回错误代码-1
}



void DisplayLinkedList(Node* L)
{
    if (L == L->next)
    {
        printf("[Blank LinkedList]\n");
    }
    else
    {
        Node* head = L->next;
        for (Node* p = head->next; p != head; p = p->next)
            printf("%d ", p->data);
        putchar('\n');
    }
}

int main()
{
    Node* l = nullptr;
    InitLinkedList(l);
    InsertLinkedList(l, 0, 4);
    InsertLinkedList(l, 0, 3);
    InsertLinkedList(l, 0, 0);
    InsertLinkedList(l, 1, 1);
    InsertLinkedList(l, 2, 2);
    InsertLinkedList(l, 5, 5);
    DisplayLinkedList(l);
}
/*
0 1 2 3 4 5
*/

循环单链表合并(尾指针表示, 带头节点)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
#include <cstdio>
#include <cstdlib>


#define ElemType int

struct Node
{
    ElemType data;
    Node* next;
};



int InitLinkedList(Node*& L)
{
    L = (Node*)malloc(sizeof(Node));
    if (!L)
        return -1;
    L->next = L;
    return 0;
}

int InsertLinkedList(Node*& L, int index, ElemType data)
{
    if (index < 0)
        return -1;
    Node* head = L->next;

    int i = -1;
    Node* p = head;
    do
    {
        if (i == index - 1)     //如果当前节点为要插入位置的前一个节点
        {
            Node* newNode = (Node*)malloc(sizeof(Node));
            if (!newNode)
                return -1;
            newNode->data = data;
            newNode->next = p->next;
            p->next = newNode;
            if (newNode->next == head)  //如果新插入的节点是尾节点, 那么把尾指针指向新节点
                L = newNode;
            return 0;
        }
        p = p->next, i++;
    } while (p != head);

    return -1;  // 如果整个循环链表中都没有目标位置, 就返回错误代码-1
}

void MergeLinkedList(Node*& La, Node*& Lb)
{
    //将b循环链表接到a循环链表的后面
    Node* aHead = La->next;
    Node* bHead = Lb->next;

    La->next = bHead->next;
    Lb->next = aHead;
    free(bHead);    //释放b循环链表的头节点
    La = Lb;
    Lb = nullptr;
}



void DisplayLinkedList(Node* L)
{
    if (L == L->next)
    {
        printf("[Blank LinkedList]\n");
    }
    else
    {
        Node* head = L->next;
        for (Node* p = head->next; p != head; p = p->next)
            printf("%d ", p->data);
        putchar('\n');
    }
}

int main()
{
    Node* l1 = nullptr, *l2=nullptr;
    InitLinkedList(l1);
    InitLinkedList(l2);
    InsertLinkedList(l1, 0, 0);
    InsertLinkedList(l1, 1, 1);
    InsertLinkedList(l1, 2, 2);
    InsertLinkedList(l1, 3, 3);
    InsertLinkedList(l1, 4, 4);
    InsertLinkedList(l2, 0, 5);
    InsertLinkedList(l2, 1, 6);
    InsertLinkedList(l2, 2, 7);
    InsertLinkedList(l2, 3, 8);
    InsertLinkedList(l2, 4, 9);
    DisplayLinkedList(l1);
    DisplayLinkedList(l2);
    MergeLinkedList(l1, l2);
    DisplayLinkedList(l1);
}
/*
0 1 2 3 4
5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
*/

栈的应用-括号匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <stack>


bool match(char const* str)
{
    std::stack<char> s;
    for (int i = 0; str[i]; i++)
    {
        if (str[i] == '(' || str[i] == '[')
            s.push(str[i]);
        else if (str[i] == ')' && s.top() == '(')
            s.pop();
        else if (str[i] == ']' && s.top() == '[')
            s.pop();
        else
            return false;
    }
    return true;
}

int main()
{
    std::cout.setf(std::ios::boolalpha);
    std::cout << match("[[()[()]]]") << std::endl;
    std::cout << match("[[()[()]])");
}
/*
true
false
*/

栈的应用-进制转换

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <cstdio>
#include <stack>

//无符号数的进制转换
void BaseConvert(unsigned base, unsigned num, char* str)
{
    std::stack<char> s;
    for (; num; num /= base)
        s.push(num % base + 0x30);	//取余并转换为ASCII码

    int i = 0;
    for(;!s.empty();s.pop(), i++)
        str[i] = s.top();
    str[i] = '\0';
}

int main()
{
    char s[32] = { 0 };
    unsigned num = 0x12345678;
    BaseConvert(2, num, s);
    printf("2进制: %s\n", s);
    BaseConvert(8, num, s);
    printf("8进制: %s\n", s);
    BaseConvert(10, num, s);
    printf("10进制: %s\n", s);
    BaseConvert(16, num, s);
    printf("16进制: %s\n", s);
}
/*
2进制: 10010001101000101011001111000
8进制: 2215053170
10进制: 305419896
16进制: 12345678
*/